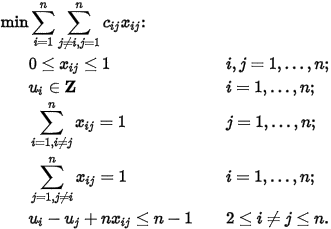Brief summary
I have interest in operations research, optimization, evolutionary algorithms, and experiments planning. My main research topic consists in the development of mathematical models and algorithms for mixed-integer linear optimization problems. Such problems are solved by exact methods, such as branch-and-bound based algorithms, dynamic programming, cutting-plane methods, or other advanced decomposition methods. Besides, heuristic algorithms, such as local search-based techniques, evolutionary algorithms and lagrangian heuristics, are also used to get good solutions for hard instances. Such methods and algorithms are generally applied to solve a class of problems, or a specific problem of great practical relevance.
I also have interest in studying evolutionary algorithms, researching new operators for different problem's classes. Besides, another interesting research field is to study the population dynamics of such algorithms, characterizing how individuals (solutions) interact with each other by means of the genetic operators.
Research topics
Heuristics
Techniques designed for quickly obtaining a solution for a problem. Heuristis are used when exact methods are too slow, or for finding an approximate solution when classic methods fail to find any exact solution. This is achieved by trading optimality, completeness, accuracy, or precision for speed.
The objective of a heuristic is to produce a solution in a reasonable time span that is good enough for solving the problem at hand. This solution may not be the best of all the actual solutions to this problem, or it may simply approximate the exact solution. But it is still valuable because finding it does not require a prohibitively long time.
Heuristics may produce results by themselves, or they may be used in conjunction with other optimization algorithms to improve their efficiency (e.g., they may be used to generate initial solutions/bounds for exact algorithms). They also can be combined with each other, resulting in hybrid heuristic methods. Besides, it is also possible to develop metaheuristics, i.e. general heuristic methods that can be applied to a wide range of problems.
Mathematical programming
Consists in developing and solving mathematical models, particularly optimization models, to assist in decision making. These models consists in optimizing a objective function of many variables, often subject to a set of constraints. Mathematical programming is usually used to find the optimal solution of a given problem. However, mathematical models can also be used as heuristic algorithms.
Several branches of mathematical programming exists:
- Linear programming: The objective function and the constraints are linear.
- Integer programming: As in linear programming, both objective function and constraints are linear. However, the solution only accepts integer-valued variables.
- Quadratic programming: The objective function is quadratic and convex, while the constraints are all linear and non-linear inequalities.
- Optimization under uncertainty: The problem data is subject to uncertainty. This uncertainty can be represented as an interval of values (or a discrete set of values) in the case of robust optimization, or as a probability function, in the case of stochastic optimization. Also, the problem can vary over time, being a dynamic optimization problem.
Evolutionary algorithms
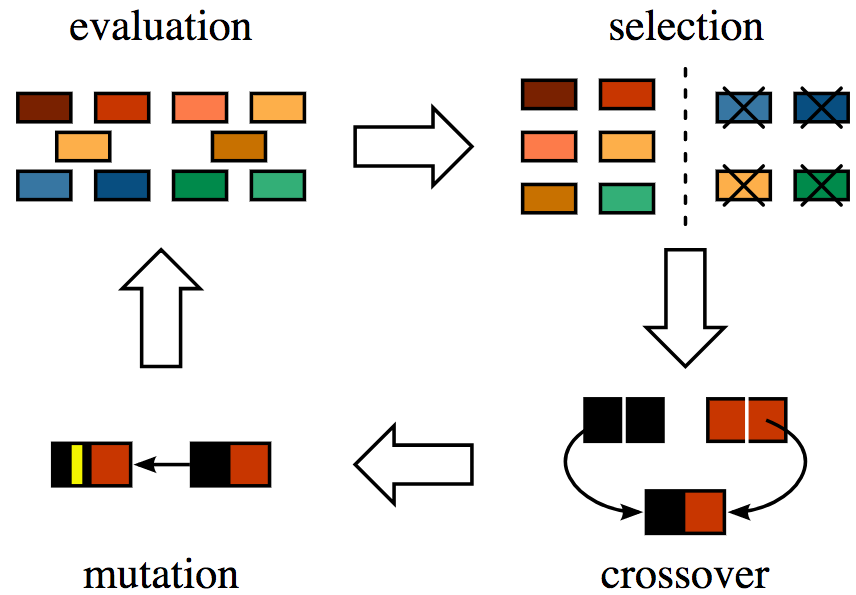
Metaheuristics that evolves a pool of solutions, called population. Each solution of this population is said to be an individual. Individuals are assigned with a fitness value, which represents the solution's quality. An Evolutinary Algorithm evolves it's population by means of genetic operators, such as reproduction, mutation, recombination, and selection. These operators are iteratively applied until a stopping criterion is met.
The key aspect when designing evolutionary algorithms is the balance between exploration and intensification. Exploration is used to explore the search space. In addition, it is also responsible to escape from local optimas. On the other hand, intensification is needed to improve promissing solutions' fitness, thus better aproximating the problem's solution.
Evolutionary algorithms often perform well approximating solutions to all types of problems. They find applications in telecommunications, engineering, economics, chemistry, among other areas, being an important computational intelligence technique.
Computational intelligence
Computational intelligence is a set methodologies and approaches that addresses complex real-world problems to which mathematical or traditional modelling can be useless. Such problems might contain some uncertainties during the process, or the process might simply be stochastic in nature. Indeed, many real-life problems cannot be translated into binary language for computers to process it. Computational Intelligence therefore provides solutions for such problems.
Evolutionary algorithms, mathematical modelling, heuristics and metaheuristics, neural networks, and fuzzy logic are the main approaches employed in computational intelligence, among other stochastic methods.